Last updated on July 14th, 2024 at 03:01 pm
CAGR Full form stands for compounded annual growth rate or CAGR and is calculated by the following formula, often used in investment decisions. It’s the average rate at which an initial total investment grows for x number of years. In this blog you can also use our CAGR Calculator to try out some examples
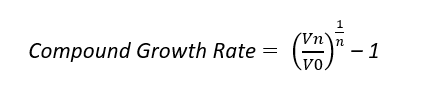
Stock CAGR Calculator Online
Use the compounded annual growth calculator below to find and calculate Compounded annual growth rate using your own examples. For your ease let me give some common examples which you can try out to understand the basic fundamentals of this return calculator.
CAGR Calculator
- In 2021 you invested $10000 in a large cap mutual fund and in 2024 you see that your portfolio value is now $50000. Was is the CAGR return in the mutual fund investments?
- You approach a mutual fund for investing $5000 every month, you begin your investment in 2020. At the end of 4 years, you have $500,000. What is the CAGR mutual fund in this case? ( Just a small tip on how to calculate CAGR for sip, please ensure that you take initial investment as 0).
CAGR Full Form
CAGR stands for compounded annual growth rate, which is a mathematical approximation to find the average rate between two periods a value has increased or decreased. The major parts of the CAGR Calculation are;
- Initial investment, also called as Present value
- The repeated investment or withdrawals like SIP or EMI’s. Which is also called as PMT.
- Annual rate of return, interest rate depending on whether it’s a liability or asset. In case of asset the rate signifies the rate at which investment has grown.
- Future value which means the either the final value of portfolio in case of investments. Or a loan which approaches a future value of zero.
And the idea here is that if you know any 3 of the above values, then you can find. For example if you know the initial value, the rate of return, number of years of compounding then you can find the future value. Hence you don’t need a separate reverse cagr calculator.
CAGR Meaning
I will cut to the chase and jump right into examples which is more helpful in understanding.
So, let’s assume you bought a piece of land in 2010 for $10000; afterwards, ten years, you end up selling at $20000. What is the Average annual growth rate ?
The usual instinct is to know if we did good, bad or ugly, right?
Now I could answer the good, bad or ugly in multiple ways;
- Times the Initial total investment: I could say I made twice what I invested.
- Percentage Change in the value: Which is to say, by how much % did it change from its initial value of $10000?
- Average rate: The average rate at the property increased in its value over ten years.
So, the correct answer depends on what makes more sense to you. None of the answers and approaches is incorrect, but here are the issues.
Firstly, option one doesn’t give you the time frame. This means if, in a similar situation, your friend had doubled the value in 5 years instead of 10, then this won’t be captured.
Secondly, option 2 suffers from the same problem as option 1, but only the format of the problem changes. E.g., My property increased in value by 50% but in how many years?
- Property Increased by 2 X
- Value increase by 100%
- The value increased at a rate of ((20000/10000)^(1/10)-1)= 7.17%. Or simply, the CAGR earned was 7.17%.
A very common confusion can be related to the (^ 1/n), which is nothing but a proportionate division of the 100% increase across ten years.
So 7.1% across ten years, but an obvious question might be 7.1% x 10 = 71% then how did the value increase by 100%?
And the answer is compounding, or interest on interest. However, I’ll keep the concept of compounding for another time.
Understanding the Annualized Rate in CAGR Calculations
When discussing the Compounded Annual Growth Rate (CAGR), it’s essential to also understand the concept of the annualized rate. The annualized rate represents the average yearly return of an investment over a specified period, accounting for the effects of compounding. For instance, if you have an investment that grows from $10,000 to $20,000 over ten years, the annualized rate will show the average rate at which the investment grows each year to reach that final value. This rate provides a more precise picture of investment performance compared to simple average returns, as it smooths out the effects of market volatility and irregular growth patterns. Understanding the annualized rate helps investors make better comparisons between different investment opportunities, ensuring a more informed decision-making process.
Comparing Investment Performance Using CAGR Calculator
When comparing the performance of different investments, the “compounded annual growth rate” (CAGR) is a crucial metric. For example, if you “invested Rs 10,000” in 2010 and the value grew to Rs 20,000 by 2020, the CAGR would reflect the “rate of growth” over this period. This metric helps investors understand how their “initial investment” has performed over time, accounting for the compounding effect. Unlike simple average returns, CAGR provides a more accurate picture of an investment’s performance by smoothing out the effects of volatility. This is essential for evaluating “investment risk” and making informed decisions about where to allocate capital.
Rule of 72 For Compounded annual growth rate
Now, you don’t want to be that guy who always opens his calculator for every such calculation. There is a very easy method by which you can approximate CAGR.
E.g.;
- At 20%, the value doubles in 3 years
- At 7%, the value doubles in 10 years
So what’s the magical way?
Simply Divide 75/(No of years)= to get an approximate CAGR.
Go ahead, try it!
You could also reverse the formula and calculate the years it takes.
For eg; 75/ 7%= 10 years, 75/20= 3 Years approx.
So 75 is the number.
How to calculate the CAGR in Excel
Chicken it is to calculate CAGR in Excel! Simply put following are how you could calculate CAGR.
- Rate Function
- Manual algebraic
- RRI Function
All are the same in output, but it varies depending on the data you are working with.
So, I’ll elaborate a little here.
Firstly, the rate function is used fully when you are dealing specifically with situations where you are also dealing with periodic additional investments or withdrawals, which is signified by the PMT(Payment Variable).

Notice that in this example, we don’t have any additional periodic investments or withdrawals hence PMT is zero. Also, notice that investment is shown with negative signs, which means outflow.
Secondly, the manual algebraic method is preferred when we are dealing with a single-cell calculation.

Thirdly the method of using RRI is good when you are not good with algebraic calculation altogether.
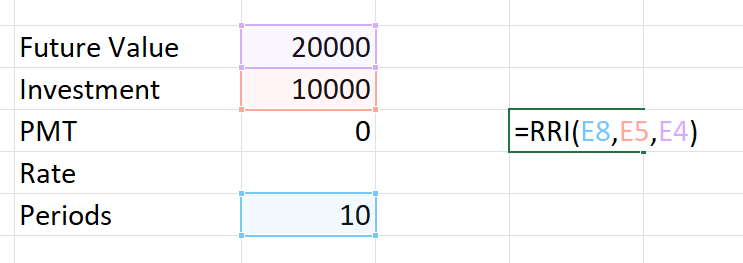
Notice that in the case of the RRI function, you don’t even have to worry about the signs. It automatically assumes that the investment value(PV) is negative.
However, in any of the three methods, the answer is the same.
Use cases of CAGR
Majorly the use cases are in economics and immense in the case of finance.
Frequently you should see the use of CAGR in GDP Growth rates or inflation rates. Similarly, in finance, you will see mostly all investments coming with the calculation of CAGR in their brochures.
So lets take some example of CAGR meaning in mutual fund case. Below is a screenshot of one of the mutual funds, and notice what it says about the return calculation.
Another interesting thing to note in these mutual fund websites, is that all of them will provide you some kind of CAGR calculator.
Example: Savings account
Imagine you have invested $10,000 in a savings account. The return for three year period of time is outlined below [1]: What is the compounded annual growth in the investment period?
| Year | Average Returns | Portfolio Value |
| 1 | 30% | $13,000 |
| 2 | 7.69% | $14,000 |
| 3 | 35.71% | $19,000 |
Solution:
As you can see, the returns for every year are not constant. By using the formula, the CAGR can be calculated as follows:
The CAGR of 23.86% over the 3-year investment can assist the investor in comparing alternatives for his capital or making forecasts of future values. Furthermore, he can even predict what his returns are going to be after a few years.

Let us look at another example where the CAGR is known to us, and we have to calculate the future value. Say you have invested $5,000 in a stock mutual fund with an average CAGR of 26%, and you want to find out your approximate returns after ten years. According to the CAGR formula, the final value will be,

After solving this, the value of the return after ten years will be approximately $50,428.
Let me give you another example of this calculator in case of share prices.
So let’s suppose in the year 2020, during the covid market correction you invested in the stock market in the TITAN industries stock. Below are The assumptions;
- The share price was INR 1043 on august 2020.
- And today in 2024 July the stock price is INR 3406.
So the what is the CAGR or compounded annual growth rate if you just bought one stock.
Importance of CAGR return calculator
CAGR is one of the most popular variables used to determine the profitability of an investment. One of CAGR’s advantages over an average rate of return is that it is not influenced by percentage changes that may yield misleading results. For example, look at the following example [3]:
| Year | Amount | Return |
| 0 | $1,000 | – |
| 1 | $1,250 | 25% |
| 2 | $937.5 | -25% |
His example shows that the portfolio’s value increased by 25% to $1,250. The following year, the returns dropped down by 25%, and the final value of the portfolio was $937.5. Even though the average returns are 0%, there is a loss of $62.5. Using these values, the CAGR comes out to be -3%. Hence the CAGR is more accurate than the average returns.
Let us look at another example where the CAGR is known, and we have to calculate the future value. Say you have invested $5,000 in a stock mutual fund with an average CAGR of 26%, and you want to find out your approximate returns after ten years. According to the formula, the final value will be,
After solving this, the value of the return after ten years will be approximately $50,428.
Limitations
There are a few disadvantages of CAGR as well. The most important limitation of CAGR is that it calculates a smoothed growth rate over a period, Hence, it ignores volatility and implies that the growth during that time was steady. Also, CAGR does not account for when an investor adds or withdraws funds from his portfolio. Another disadvantage of CAGR is that it only represents past growth, and the investor cannot assume that the CAGR will be the same in the future as well. [3]
A third limitation of CAGR is its representation. Say that an investment fund was worth $10,000 in 2016, $7,100 in 2017, $4,400 in 2018, $8,100 in 2019, and $12,600 in 2020. In 2021, the fund manager will represent that the CAGR was a whopping 42.01% over the past three years, but when it comes to the CAGR over the past five years, it is only 4.73%. [1]
What is a good CAGR?
The interpretation of CAGR will vary on the context. For example, if you are looking at a real estate investment opportunity then your expectation would be a minimum 8-9% CAGR. While at the same time, the expectation from stock investments would be at least 15% CAGR.
Is 7% Mutual fund CAGR calculated good for investments?
In case we are looking at investment portfolio returns, then a 7% CAGR is not good because the government bonds rate itself is 7.25% on a risk-adjusted basis. We have to look at things in context. E.g., a 20% CAGR for three years means your money doubles every three years. Rarely can anyone sustain such higher returns consistently for long periods? Hence in terms of investing, anything above 15% CAGR is superb. The rest is putting in the money and letting it work, and being patient.
Compounded annual growth rate calculations are very common in financial modeling.
How to calculate CAGR in a normal calculator?
If you are talking about a regular calculator without any rate, PMT, future value functionality. Then you can use the following steps to calculate CAGR in a normal calculator;
- Divide the final value of investment buy the initial investment. For example if you invested $100 and you withdrew $200. Then divide 200/100= 2.
- Now, if we just interpret two then what it means is that the invest doubled in value.
- Next we want to calculate annualised return. So let’s say this money double in 3 years. Hence if we want to annualise it into an average return for a year. Then we divide 1/3. Which comes upto be 33.33%
- Now just don this final calculation, 2 ^( 0.33)-1= 25% approximate average returns.
Conclusion:
CAGR is a very useful method to calculate the growth rate of an investment. It can be used to evaluate past returns or predict the future returns of your investments. However, remember that CAGR works suitably only for lumpsum investments. Investors can analyze investment alternatives by comparing their CAGRs from identical periods. Also, a direct conclusion is that the higher the return, the higher the future value. So if you keep your capital in a savings account with a 4% annual return versus a 12% rate every year in a mutual fund portfolio, the value will be higher with the higher rate of return.
Related Articles



