A very simple way to understand annual return is to actually calculate it. Mostly, everyone who has invested any amount in any asset would be interested in knowing a relative percentage earned. However, there are some complications to it, which is why this article exists. So let’s get started
What is Annual Return?
So, annual return is a percentage calculated on the excess or less generated over a base value. Also, since we are talking about annual, hence the calculation is time sensitive.
Annual Return Examples with Calculation
So, let me explain this by giving you some examples which is the best way to understand annual return calculation.
Example 1: Annual Return Earned with Stocks over 1 year period
So lets suppose Mrs. Jhanvi, invested $500 in stock A on 1ST April 2023. On 31ST March 2024 the stock appreciated in value to $600. What is the annual return?
So as you can see I am interested in knowing the return percentage.
- Base value here = $500
- Excess over base Value= $600- $500= + $100
- Time period : 12 months or 1 Year or 365 Days
Now let’s suppose the time period chosen is 1 year. Or I am asking the amount of return generated in one year.
So the calculation would be; Ending value/ Base value-1 or $600/$500-1. Which is nothing but 20%.
Example 2: Annual Returned Earned over more than one year period
Now, remember in the first example I kept things simple, which is why it was just a simple calculation. But now let me complicate things furter. What If I am interested in knowing the annual return over 2 year period instead of 1?
So keeping everything same, now the calculation would be as follows;
Annual return= (Ending value/ Base Value)^(1/n)-1
Now before you become confused let me explained what (1/n) means. Since now the ending stock value was after 2 years instead of 1, hence if we just do (1/1) then it would mean 1 year. But, this return was generated over 2 year period, so the calculation would be (1/2) or 0.5. Which means we are asking that $500 became $600 in 2 years, but what would be the annual rate of return. Hence it is ½ or 0.5.
So the answer would 9.54%. or we are saying that over a 2 year period the stock generated an annual return of 9.54% annually.
Annual Return Formula & Variations
Formula for Annual Return
Now, let me summarize this formula of annual return mathematically.

Where, Ending value is the final value including dividends, appreciation etc. Beginning is the initial investment. N is the total period of investment and redemption . While -1 is done to calculate the actual percentage.
Variations in Annual Return Formula
Now that you understand the basics of this formula, you can basically change the time period under question.
Daily Compounded Return
So, what if someone asks you this questions. Mr. X invested $100 and by the end of the year in one year the stock became $150. What was the average daily compounding rate?
Again come back to the basics
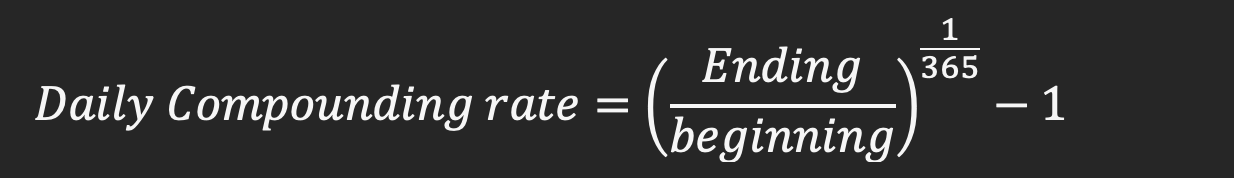
If you plugin the values
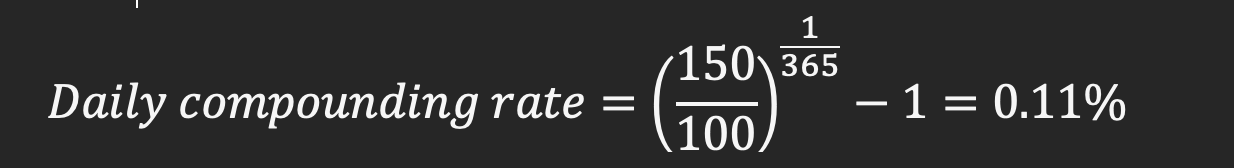
Hence what you are implying here is that on an average the money was compounding at a rate of 0.11% daily.
Semi Annual Compounded Return

Let me stick with the same example and again ask a different question. What is the semi-annual compounded return
Or semi annual compounding of 22.47%
Common Mistakes In Calculating Annual Return
So, what I have seen people commonly making a mistake with this formula is with incorrect periods. So let me summarize it;
- For half yearly, the n should be 2 not 6. Because there are 2 half years in a year.
- Similary for monthly the n should 12. 1/12.
- For quarters we have 4 quarters, hence ¼.
- Likewise for daily it can be either 240 or 365. Usually I take 240, if it’s a stock or trading instruments
- Another big mistake that 4 in 5 people make is not using the brackets properly. Notice below in the image that 1/n, -1 and 500/200 are all different items, hence you should use proper brackets to distinguish them

Real World Cases
Loans
Usually when you take a loan the rate of interest quoted is annual. For eg; an annual rate of 9.35%. However, since you pay your EMI monthly, the rate of interest is higher than 9.35%
Check this calculation:
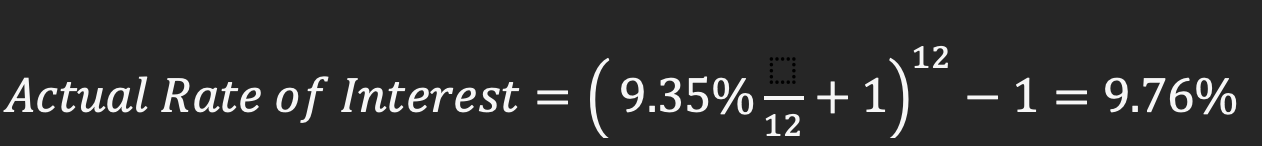
Hence the actual rate of interest paid is 9.76% not 9.35%
Mutual Funds
Most of the pooled investment vehicles generally quote the XIRR, which is nothing but again an average annual return. However be care full to check which period has been used. Since, we know that beginning value has a huge influence on the rate of return. So, if the beginning value has been taken from a period where the stock market had crashed then the return will be high. Compared to if it was taken when the market was at the highest point.

