So, Interest is a monetary charge levied on borrowed money and it is represented as an annual percentage rate. Interest is the amount of money the lender receives for lending out money. So ,There are two types of interests: Simple Interests and Compound Interests. Let us look at both these types and what the differences are between the two.In this article we discuss, compound interest and simple interest formula.
Simple interest means that you get 8% on the same original investment of $100, versus compound Interest which would calculate 8% on the increased value of $108
What is Simple Interest?
So, Simple interest, as the name suggests, is an easy and simple method of calculating interest on borrowed capital. Furthermore, in simple interest, the principal amount remains constant. . When you make an interest payment, the payment goes towards that month’s interest and the remainder goes to the capital so that the interest never accrues. It is a benefit to the customer when they pay their simple interests on time or early every month. For example ;Auto loans, short-term loans, and mortgages are simple interest loans.
The formula for simple interest and amount to be repaid:
S.I. = (P×N×R)/100 Amount = Principal + S.I.
P = Principal Amount
N = No. of years (Period of time)
R = Rate of Interest
A = Amount (S.I. + Principal amount)
Let’s look at an example.
Bob takes a car loan of $18,000 with a 6% interest for 3 years. The simple interest would be
=(P×N×R) / 100 = (18000×3×6) / 100 = $3240
Total Amount to be repaid will be 18000 + 3240 = $21,240
What is Compound Interest?
So, Compound interest is the interest on a loan calculated Based on both the initial principal and the accumulated interests from previous periods.
Furthermore, to simple interest, in compound interest, the interest adds to the principal amount every year . To give you a better understanding of this, consider that you have deposited ₹1000 in a bank at 10% interest.
Now, according to simple interest and compound interest, the earnings for the first year would be 10% of 1000, which amounts to ₹100. In the case of simple interest, you will earn ₹100 in the second year as well. However,in compound interest, an interesting phenomenon occurs. The interest gets added to the principal amount each time. As a result, the new principal amount becomes ₹1100. Consequently, you would be earning 10% on ₹1100, in contrast to ₹1000. Therefore, your earnings in the second year would be ₹110.
Einstein once said, “Compounding is the world’s eighth Wonder!” Moreover, this is precisely what he was talking about. In fact, compound interest has the remarkable ability to make your sum grow at a much faster rate than simple interest. Additionally, the rate at which compound interest accrues differs based on the frequency of compounding, such as monthly, quarterly, semi-annually, or annually. This is because the interest-on-interest effect can generate more positive returns.
The formula for Compound Interest
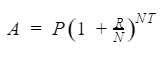
Amount = Final Amount
P = Principal Value
R = Interest Rate
N = Number of times interest is applied per year
T = Total number of years.
Let’s take the same example as taken in simple interest but this time Bob will be investing $18,000 in a bank at 6% interest given quarterly for 3 years. As the interest is paid quarterly, N = 4. The final amount would be
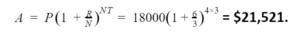
As you can see by the compounding effect, the final amount is $281 more than the Simple Interest amount.
Uses of these Calculations
So, There is a reason why compounding got this title for itself.
Just to give you a birds-eye view of what compounding can do, if you had invested any amount of money in the year 2000 in the NIFTY 50 index that amount would be at least 10 x by now.
While, there is a lot you can do or lose if you don’t understand this concept practically.
For example:
- Loan Calculation: When we take any form of the term loan, compounding calculations kick in. Also, Look at the image below on what an 8% home loan rate versus paying interest at 9% can do to the total payment over time.
Hence,Retirement Planning: Let’s say you want to calculate, how much money you need to save every month to make sure you maintain your current lifestyle. Notice what happens when the return expectations increase from 11% to 15%. So, Your monthly investments required become 1/3. There will also be significant differences when we change the assumption from compounded monthly to compounded annually.
| Parameters | Details | |
| Age | 30 | |
| Retirement | 60 | |
| Life expectancy | 80 | 20 |
| Current Expenses | 40000 | |
| Current inflation | 6% | |
| Future value of current expenses | 229739.6469 | |
| Returns Expected | 11% | 15% |
| Post Retirement Inflation | 3% | |
| Funds Required at Retirement | ₹ 4,14,24,565.81 | ₹ 4,14,24,565.81 |
| Investment Per Month | ₹ -14,770.65 | ₹ -5,983.37 |
Simple-interest-vs-compound-interest
Firstly , I have listed the key differences between simple interest vs Compound interest below.
| Difference | Compound Interest | Simple Interest |
|---|---|---|
| Calculation | Interest is calculated on both the initial principal amount and accumulated interest. | Interest is calculated only on the initial principal amount. |
| Growth | The interest earned is added to the principal, resulting in exponential growth over time. | The interest earned remains constant throughout the investment period. |
| Earnings | Higher earnings due to the compounding effect over time. | Lower earnings compared to compound interest. |
| Application | Commonly used in long-term investments or loans. | Generally used for short-term loans or investments. |
| Formula | A = P(1 + r/n)^(nt) | A = P(1 + rt) |
Note:
- A = Total amount including principal and interest
- P = Principal amount
- r = Annual interest rate (in decimal form)
- n = Number of times interest is compounded per year
- t = Number of years
Please note that the formulas provided are for annual compounding. Compound interest can be compounded more frequently, such as monthly or quarterly, by adjusting the formula accordingly.
Compounding Periods
Compounding periods refer to the frequency at which interest is calculated and added to the principal amount in an investment or loan. The more frequent the compounding, the faster your money can grow. This is an important aspect to understand In the context of,compound interest and simple interest formula.
For instance, imagine you invest $1000 in a savings account. The interest on this account can be compounded annually, semi-annually, quarterly, monthly, or even daily. When interest compounds annually, it’s calculated once a year. But if it compounds quarterly, it’s calculated four times a year, and so on.
The benefit of more frequent compounding is that you earn interest not only on your initial investment but also on the interest that’s already been added to the principal. This creates a snowball effect, where your money grows faster over time. Transitioning from annual to quarterly compounding, for example, means you’ll earn a bit more each quarter because the interest is compounding more often.
To put it in perspective, let’s say you have two accounts, both with a 5% annual interest rate, but one compounds annually and the other compounds quarterly. In the annual compounding account, after a year, you’ll have $1050. However, in the quarterly compounding account, after a year, you’ll have around $1051.34. The extra growth comes from the fact that the quarterly compounding account is calculating and adding interest more frequently.
In summary, compounding periods determine how often your interest is recalculated and added to your investment. The more frequent the compounding, the more your money can grow over time due to the compounding effect. So, it’s generally beneficial to choose an investment that compounds more frequently, as long as other factors like interest rates and fees remain favorable.
Rule of 72
The Rule of 72 is a simple and handy financial tool to estimate how long it will take for an investment to double in value, based on a fixed annual rate of return. It’s a quick mental calculation that provides a rough estimate.
To use the Rule of 72, divide 72 by the annual interest rate or growth rate. The result will give you an approximate number of years it would take for your investment to double. For instance, if you have an investment with an annual return of 8%, according to the Rule of 72, it would take around 9 years for your investment to double (72 ÷ 8 = 9).
While the Rule of 72 isn’t 100% precise, it’s remarkably close for interest rates between 6% and 10%. It’s a valuable tool for making quick projections and assessing the potential growth of your investments over time. Just remember that it’s a simplified formula and doesn’t account for factors like taxes, compounding frequency, or varying rates of return.
In summary, the Rule of 72 is a nifty formula that provides a quick estimate of how long it takes for an investment to double by dividing 72 by the annual interest rate. It’s a helpful tool for making rough calculations about the growth of your investments and making informed financial decisions.
Real World Applications of Compound interest and Simple Interest Formula
imple interest and compound interest are fundamental concepts in finance with practical applications in everyday life.
Simple Interest:
Simple interest is often used in scenarios where loans or debts are involved. For instance, if you borrow $1000 from a friend and agree to pay back 5% interest annually, the interest for the first year would be $50 (1000 * 0.05). You’ll pay back a total of $1050 after the first year. The next year, the interest will still be $50, regardless of how much you’ve paid so far.
Compound Interest:
Compound interest has broader applications, especially in investments and savings accounts. Let’s say you invest $5000 in a savings account with a 6% annual interest rate compounded annually. After the first year, you’d earn $300 in interest (5000 * 0.06), making your total $5300. In the second year, however, you’d earn 6% interest not just on the initial $5000, but on the new total of $5300, leading to an interest of $318. This compounding effect continues to grow your investment significantly over time.
Another example is a mortgage. When you take out a mortgage to buy a house, the interest you pay is often compounded monthly. This means that a portion of your monthly payment goes toward both the principal (the original loan amount) and the interest. Over time, as the outstanding balance decreases, the interest portion becomes smaller, allowing you to pay off more of the principal.
In summary, simple interest is frequently used in straightforward loan scenarios, while compound interest plays a vital role in investments, savings, and loans that involve changing balances over time. Understanding these concepts helps individuals make informed financial decisions in various situations.
Conclusion
The major difference between simple interest and compound interest is that in simple interest the principal amount remains the same throughout the entire duration whereas in the compound interest the interest gets added to the principal amount every time. Hence, this drastically affects the final amount which one would get after the maturity period. Also, These types of interests are widely used in many financial services for banking purposes. Loans such as car loans, educational loans, and instalment loans use simple interest. Also,the compounding interest is used by savings bank accounts, FDs, mutual funds etc.