Last updated on December 27th, 2022 at 03:13 pm
What is the Black-Scholes-Merton Model?
The Black-Scholes-Merton is a pricing model for financial instruments. This model is used for the valuation of stock options. The Black-Scholes-Merton Model (BSM) is used to determine the fair prices of stock options based on six variables: volatility, type, underlying stock price, strike price, time, and the risk-free rate. The BSM is based on the principle of hedging and focuses on eliminating risks associated with the volatility of underlying assets and stock options.
Equation of the Black-Scholes-Merton Model
The BSM model can be described as a second-order partial differential equation.

This equation describes the price of stocks options over time.
- Pricing a Call Option:
The price of a call option C is given by the following formula:
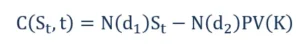
Where:
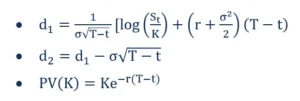
- Putting a Put Option:
The price of a put option P is given by the following formula:
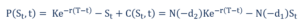
Where:
N – Cumulative distribution function of normal distribution
T-t – Time to Maturity
St – Spot price of the underlying asset
K – Strike price
R – Risk-free rate
O – Volatility of returns of the underlying asset
Assumptions of the Black-Scholes-Merton Model
- Lognormal distribution: The BSM model assumes that stock prices follow a lognormal distribution.
- No dividends: The BSM model assumes that the stocks do not pay any dividends or returns
- Expiration date: The model assumes that the options can only be exercised on their expiration or maturity date.
- Random walk: State of random walk is assumed as the market is volatile and cannot be predicted.
- Frictionless market: No transaction costs, including commission and brokerage, is assumed in the BSM model
- Risk-free interest market: The interest rate is assumed to be constant, hence making the underlying asset a risk-free one.



