Last updated on October 23rd, 2024 at 03:48 pm
Harmonic mean formula is = n/{(1/x1)+(1/x2)+(1/x3)+…..+(1/xn)}, and application of harmonic mean is in speed & Ratio based calculations.
In statistics, data science or just general everyday decisions, we always are interested in knowing the middle value.
Like what’re the average marks, average speed or average returns etc.
In technical terms, we also call it central tendency.
I will try to make this article as practical and easy as possible. So hang on and read till the end.
Applications of Harmonic Mean Formula Example
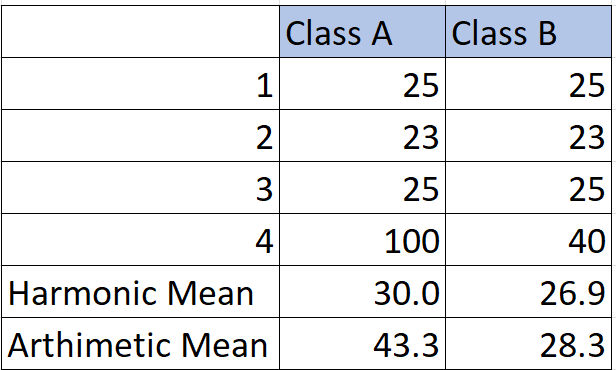
Consider the following example Class A students and Class B students. You want to find out what’s the average score of students. However, there is a problem, which is that in class A students, there is one student who has got 100. So how is that a problem?
Well, that one score shoots up the average and gives you a false sense of performance.
So, the solution to that is Harmonic Mean.
- Which will give a lesser weightage to the extreme values
- More weightage to the regular non-extreme values.
Making the average measurement more reliable.
So what’s important for you to remember is, when it is used.
When the data has larger extreme values.
Harmonic Mean Formula
Now, as discussed in the last part, regarding giving less weightage to the larger extreme values?
Hence we need to understand first the weightage process of normal arithmetic.
- This is equal to the case of a normal average; in other words, if we have four data observations, then each has 25%.
- The harmonic process is exactly the opposite; we take the reverse of the values, i.e. Class A (1/25+1/23…..+1/100).
- Hence you can observe that 100, a larger extreme value, becomes even smaller.
- So 25 gets a weightage of 4%, 100 gets a weightage of 1%
- Next, we added up all the reversed values (1/25+1/23/+1/25+1/100)=0.13
- Divide N/( 0.13)= 4/0.13 which equals 29.96.
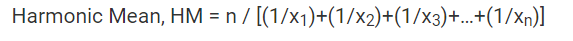
Measuring Central Tendency with Harmonic Mean
The harmonic mean is a robust measure of central tendency, especially useful when the data set includes large outliers. By averaging the reciprocals of the data points, the harmonic mean gives a more accurate representation of the central value, particularly in scenarios involving rates and ratios. This method is rigidly defined and provides consistency across various applications.
3 Harmonic Mean Formula Applications
Every time you come across a situation to check if harmonic means can be used, follow the below rule.
The harmonic mean is used when a fixed quantity is repeatedly applied for a result.
Application 1: Finding the average speed of Cars
Let me take an example here. What should be the average speed?
- Reverse the speed values : 3/(1/10+1/20+1/30)= 16.36 Km/Hr
Application 2: Investing in Mutual funds across Periods
Again, notice here that the investment amount must be the same across periods.
So, for example, You invest $5000 across five periods, with the purchase price of a mutual fund being $100, $200, $75, $150, or $300. What’s the average price per unit?
So, the solution would be:5/ (1/100+1/200+1/75+1/150+1/300)
You can test the values and check that the simple average gives a wrong answer for total investments.
Application 3: P/E Ratio
So I plotted the Harmonic Mean of the NIFTY PE Ratio using the harmonic mean and simple average. Notice how initially HM and AM are identical, but as we keep progressing, adding more values then the simple average overestimates the mean. Hence harmonic mean makes more sense.
The Relationship of Harmonic Mean, Arithmetic Mean, Geometric Mean
The above three means are also called Pythagorean means.
You might be wondering, am I going to make this complicated? Not.
However, let’s try to play a little with numbers.
- Arithmetic Mean: a +b /2
- Geometric Mean:√ab
- Harmonic Mean: 2/(1/a+ 1/b) or 2 ab/(a+b)
So we can replace 2ab with geometric mean square because GM is √ab.
- Therefore, harmonic mean = 2 (GM)²/(a+b)
but 2/(a+b) can also be said to reverse AM.
Hence, Harmonic Mean= (GM)²/AM
Harmonic Mean Formula Vs. Mean/Median & Mode
By the way, the arithmetic mean is also called mean in general parlance. Also, the concept of median and mode, which of course, is not a part of this article, but I will share some quick light.
All that median is trying to do is to find the middle position (N+1)/2 in case of an odd number of total observations, while the N/2 position is in case of even. This needs to happen while the data is arranged in ascending order.
Why? How else would the position make sense right?
Similarly, the model is trying to find the data which repeats itself the most.
So frequency is what we are trying to find.
In summary, it means is the
- Mean: algebraic addition divided by the no of observations
- Media: Is the middle position of data arranged in an ascending order
- Mode: The data that repeats itself the most
Uses of Harmonic Mean Formula
Given below are some of the popular uses of the harmonic mean
- It can be used in speed calculation because speed is already a ratio of distance over time.
- Heavily used in finance when dealing with multiple
- It can be used to finance patterns in the Fibonacci series
- Very helpful when dealing with data which has larger extreme values
Weighted Harmonic Mean for More Accurate Analysis
In certain scenarios, it’s beneficial to apply a set of weights to the harmonic mean to reflect the importance of different data points. This weighted harmonic mean ensures that the calculation accounts for varying significance among the values, providing a more nuanced and precise result. This approach is particularly useful in finance and investment analysis, where not all data points carry equal importance.
Weighted Harmonic Mean Formula
This is just a special case, where along with finding the mean, we also wish to assign weightage.
However, all the weights should add up to 1.
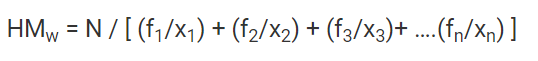
So, all that changed from our previous formula, instead of just reciprocal. We know are dividing it by the weightage.
An unweighted harmonic mean(HM), assigns equal weightage to all values, right?
However, if you wish to assign weightage, then you could use this method.
Just to add here, this is not a special case of just harmonic mean, but you could also find weighted arithmetic mean too.
Advantages of Harmonic Mean Formula Versus Averages
Consider that you are evaluating a mutual fund investment scheme. Which one of the below questions will you be interested in asking?
- What was the highest return for a particular month?
2. Or what have been the average returns?
Let’s take the example on this sheet: Franklin Templeton MF.
Average | Median |
0.58% | 1.02% |
After the analysis, we concluded that the average monthly return is:
- Does the central location itself give you any information?
- What if we were to find how much each day fluctuates from the centre?
- Because we are always interested in the average fluctuation, which will somehow affect our capital volatility.
- Imagine investing in a fund, and even though the returns are good at 21% annual.
- Just when you were planning to buy a house, the fund experienced a -70% fluctuation.
- This is why we are learning statistics and managing risk is more important than targeting returns.
Harmonic Mean Formula Additional Examples
Application of Harmonic Mean Example -1
You have to find the harmonic mean of the average P/E ratio of the index of the stocks of Company A and Company B.
- Company A has a market capitalization of US$1 billion and earnings of US$20 million.
- Company B has a market capitalization of US$20 billion and earnings of US$5 billion.
- The index comprises 40% of Company A and 60% of Company B.
We first need to calculate the P/E of each company.
The calculation can be done in the following way:
- P/E (Company A) = ($1 billion) / ($20 million) = 50
- P/E (Company B) = ($20 billion) / ($5 billion) = 4
We must use the weighted harmonic mean to calculate the P/E ratio of the Index.
Using the formula for the weighted harmonic mean, the P/E ratio of the index can be found:
P/E(Index) = (0.4+0.6) / (0.4/50 + 0.6/4) = 6.33
Application of Harmonic MeanExample-2
This central tendency method is particularly useful for rates or ratios. For example, look at the harmonic mean of P/E Ratios of Nifty
What this does is the exact opposite of the weighted mean.
The higher the value, the lower the proportion.
If you had calculated the average rate of P/E, how would you calculate it? You would have got 30 and if you had calculated the Weighted mean you would have got 32.
P/E Ratios- nifty | Inverse Value(1/x) |
25 | 4% |
35 | 3% |
40 | 3% |
20 | 5% |
Sum of Inverse | 14% |
HM (no of obs/ sum of inverse) | 27.86 |
Harmonic Mean Formula in Excel?
Calculating the harmonic mean in excel is easy because it saves the trouble of manually finding the inverse using the harmonic mean.
God bless bill gates for creating spreadsheets!
However a word of caution, the harmonic mean doesn’t work with negative or zero values.
You can practice this in this template:
Advantages of Harmonic Mean
While we saw how to calculate this and, at the same time, learnt when to use it.
Now its time to look at its advantages:
- It’s appropriate for the time and rate calculation
- It can be useful for derived mathematical calculation
- The harmonic mean isn’t affected by the outliers
Disadvantages of Harmonic Mean
Of course, nothing comes without some shortcomings, and this method likewise has some challenges.
- The method is complex.
- It gets affected by extreme values in opposite situations to the arithmetic mean.
Harmonic Mean Vs Geometric Mean
- Calculation Method: The harmonic mean and geometric mean differ in their calculation methods. The harmonic mean is calculated by dividing the number of values by the sum of their reciprocals, while the geometric mean is derived by taking the nth root of the product of the values.
- Data Distribution: The two means respond differently to the distribution of the data. The harmonic mean is affected by extreme values or outliers as it heavily depends on the reciprocals of the data points. On the other hand, the geometric mean is less sensitive to outliers and is suitable for data that follows a logarithmic or exponential distribution.
- Weighting: The harmonic mean assigns equal weight to each value in the dataset, treating all values as equally important. In contrast, the geometric mean can be weighted differently based on the relative importance of each value. This allows the geometric mean to give more significance to certain values compared to others.
- Interpretation: The harmonic mean is commonly used to calculate averages of rates or ratios. For example, it is useful in determining average speeds, average rates of return, or average cost per unit. The geometric mean, on the other hand, is often used to calculate growth rates, compound interest, or average rates of change over time.
- Effect of Zero Values: When zero values are present in the dataset, the harmonic mean is undefined since it involves dividing by zero. In contrast, the geometric mean can still be calculated with zero values, but it will result in a geometric mean of zero.
Conclusion
Central tendency is a large and wide concept, having its application in modern-day machine learning.
It is important to understand the core objective of calculating central tendency, without which you can make some serious errors with your decisions. Imagine that you are deciding to invest $100 Mn in an investment opportunity while concluding its average risk.
Selecting an inappropriate method of calculation could mean disaster. Similarly, imagine you are trying to measure the chance of failure for a business project, and we casually look at a skewed sample.
The skewed sample might contain data from only successful projects and not failures.
Moreover, it is also possible that the data has a time bias, which was particularly favourable for this project. On the contrary, this could also be true with a data set that contains only failures.
You see, it’s not about calculating a value; it’s about what exactly we intend to do with that value.
We are in an education system that casually deals with concepts and fundamentals without any heed to their real-world relevance. Hence it’s important that as students of maths, finance or science, you push beyond what the curriculum draws on.
