Last updated on July 28th, 2024 at 04:07 am
Fisher equation states that the nominal interest rate (r) is equal to the real interest rate (r*) plus the expected rate of inflation (π).
What is the Fisher Equation?
The Fisher equation explains the relation between the nominal and real interest rates under the influence of inflation. This equation is named after an American economist, Irving Fisher. The equation states that the nominal rate is equal to the sum of the real interest plus inflation. The equation is often used in situations where the investors ask for additional rewards to compensate for losses in purchasing power due to high inflation. It is a widely used concept in the field of economics and finance. It is mainly used in the calculation of return on investments or in predicting the behaviour of nominal and real interest rates. It is also used to compare the actual rate of interest on investment with respect to the effect of inflation.
Fisher Equation Formula
The fisher equation is expressed through the following formula:
(1 + i) = (1 +r)(1 + π)
Where:
- i – Nominal interest rate
- r – Real interest rate
- π – Inflation rate
Example
Let’s take a look at an example of the Fisher equation
Bob owns an investment portfolio. Last year, that portfolio earned a return of 3.25%. However, last year’s inflation rate was around 2%. Bob wants to determine the real return he earned from his portfolio. In order to find the real rate of return, we use the Fisher equation.
(1 + i) = (1 +r)(1 + π)
We can rearrange the equation to find the real interest rate:
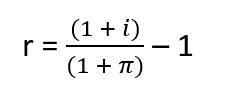
Therefore, the real interest rate or actual return on investment of the portfolio equals
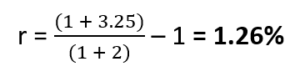
This means that Bob’s portfolio earned 1.26% last year.
The Role of Central Banks in Managing Interest Rates and Inflation
Central banks play a pivotal role in managing the relationship between interest rates and inflation through monetary policy. By adjusting the money supply and setting nominal interest rates, central banks can influence the expected inflation rate and real interest rates. This intervention helps stabilize the economy, control inflation, and promote sustainable growth. The Fisher equation serves as a critical tool for central banks to forecast the effects of their policies on inflation and interest rates.
Understanding the Relationship Between Nominal Interest Rates and Real Interest Rates
The Fisher equation underscores the relationship between nominal interest rates and real interest rates, adjusted for inflation. This understanding is vital for investors as it allows them to assess the true value of their returns. For example, if the nominal interest rate is high but inflation is also high, the real interest rate might be low, indicating lower actual earnings. By considering both nominal and real interest rates, investors can make more informed decisions about where to allocate their resources.

